Depth of Investigation#
In geophysics, “depth of investigation” refers to the maximum depth below the surface from which a geophysical survey can reliably measure. It depends on factors like the survey design and physical properties of the subsurface material. Several strategies have been proposed to assess uncertainties in models recovered from inversion. Nabighian and Macnae [NM89] used a skin depth approach for electromagnetic surveys, assuming a background halfspace resistivity. Li Y. and Oldenburg [LYO99] implemented a cut-off value based on two inverted models obtained with slightly different assumptions. A.V. and E. [AVE12] proposed a mask based on the sum-square of sensitivities to estimate a volume of low confidence. In the following, we discuss the algorithm and implementation of the sensitivity cutoff strategy.
Sensitivities#
The sensitivity matrix is calculated as part of the optimization problem solved by SimPEG while inverting geophysical data. The sensitivity matrix represents the degree to which each predicted datum changes with respect to a perturbation in each model cell. It is given in matrix form by
where \(\mathbf{m}\) is the model vector, and \(F(\mathbf{m})\) represents the forward modelling operation as a function of the model. The sensitivity matrix \(\mathbf{J}\) is a dense array with dimensions \(N\times M\), where \(N\) is the number of data and \(M\) are the number of mesh cells.
The depth of investigation mask is a property of the cells of the mesh only so the rows of the sensitivity matrix (data) are sum-square normalized as follows.
where \(w_n\) are the data uncertainties associated with the \(n^{th}\) datum.
The resulting vector \(J_{norm}\) can then be thought of as the degree to which the aggregate data changes due to a small perturbation in each model cell. The depth of investigation mask is then computed by thresholding those sensitivities
Thresholding#
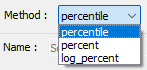
The depth of investigation can be estimated by assigning a threshold on the sum-squared sensitivity vector. This can be done as a percentile, percentage, or log-percentage. In the percentile method, the mask is formed by eliminating all cells in which the sensitivity falls below the lowest \(n\)% of the number of data where \(n\) is the chosen cutoff. In the percent method the data are transformed into a percentage of the largest value
and the mask is formed by eliminating all cells in which the sensitivity falls below the lowest \(n\)% of the data values where \(n\) is the chosen cutoff. Finally, the log-percent mask transforms the data into log-space before carrying out the percentage thresholding described above.
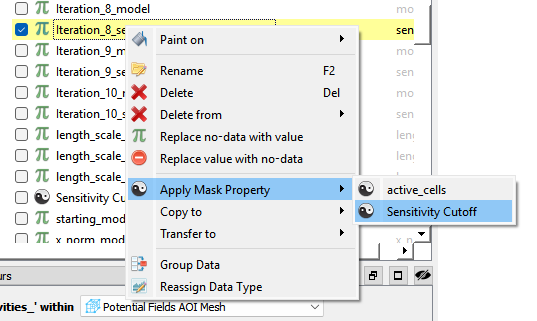
Usage#
The depth of investigation methods based on sensitivity cutoffs described above are exposed to Geoscience ANALYST Pro Geophysics users through a ui.json interface. In order to save the sensitivities during a SimPEG inversion, the ‘Save sensitivities’ option must be selected from the ‘Optional parameters’ tab of the SimPEG inversion ui.json window.
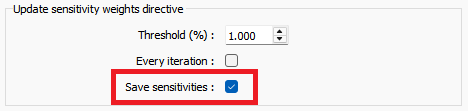
This will result in a new model generated and saved into the computational mesh at each iteration.
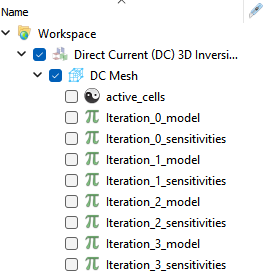
The ui.json interface allows the user to select a mesh from the simpeg-drivers result and any of the generated sensitivity models, a cutoff threshold, method, and optional name for the output.
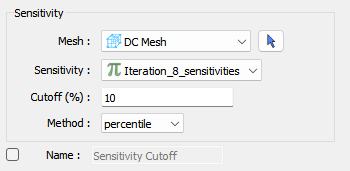
The cutoff methods are selectable in the dropdown
Whatever the options, the application will create a sensitivity cutoff mask saved on the mesh
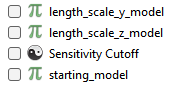
which can then be applied to any of the iterations to show only the cells that exceeded the sensitivity threshold.